sine arc function?

[midnite13]

Hello...

I was wondering if turing has a predefined sine arc function (I need it in degrees)

the sind function only returns the ratio, but it's the angle that I want. I'm not sure my wording is the best, so I'll provide an example

sind (30) would return a value of 0.5, however, I"m wondering if there's an arcsind that woudl allow for

arcsind (0.5) which would return 30.

Thanks for all your help

[MysticVegeta]

midnite13 wrote:

Hello...

I was wondering if turing has a predefined sine arc function (I need it in degrees)

the sind function only returns the ratio, but it's the angle that I want. I'm not sure my wording is the best, so I'll provide an example

sind (30) would return a value of 0.5, however, I"m wondering if there's an arcsind that woudl allow for

arcsind (0.5) which would return 30.

Thanks for all your help

you know arcsind does work.

[Saad85]

if not that then you could go arcsin*(180/pi) to turn radians into degrees

[MysticVegeta]

What I forgot to mention is that,

arcsind

works for Turing 4.05 only.

[Phonon]

I have an older version of Turing. I plan on getting the newest one but I need to get this done. The version I have does include an arctan function. Is there any way to manipulate trigonometric functions so that I can use a combination of arctan and other functions to get arcsin? I can't see a way of doing this with Taylor series expansions. Maybe I should be thinking about using exponentials and complex variables (but leaving 'i' out of it)?

[Delos]

Disclaimer: I am not a Math major. The furthest math I took was 1st year intro calculus. I don't really like math all that much - but I am quite capable of it. Take this proof with a bit of salt, and perhaps oregano for taste.

I'll going to work in radians, because I want to and because all the cool people do so anyway. You've already seen a way to convert from radians to degrees above.
Conversions from arctan to arcsin are possible, but you'll just have to limit yourself to (-1<= x <= 1). That's not too difficult. You can always manipulate your answer later on to suit your needs.

Either way:

math:

let x be inputted value let a be (x / sqrt (x^2 + 1)) arcsin (x)  = arctan (x) - arctan (sqrt (1 - x^2) / x) + arctan (sqrt (1 - a^2)/a)

Try it. It should work.

[NikG]

I'm just wondering... what exactly is arcsin even necessary for anyways?
I mean if you're just looking for the angle in between 2 lines, arctand is more than sufficient.

[Andy]

wow delos.. you're trying wayyyyyyyyyyy too hard....

consider the following:

what is sine? draw a unit circle with the centre as the origin, and start from (1,0) then walk B units counter clock wise, now let's call that point (a,b)



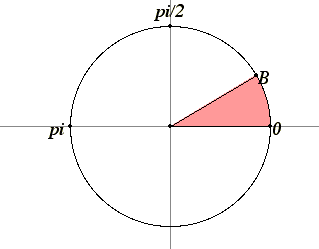
sin(B) in this case would be b. insimpler terms, sin(theta) yeilds the y co ordinate on a unit circle

to find arcsin(A):

let arcsin(A) = B => sin(B) = A

this means that A is the y co ordinate of the arc length B from the (1,0) along the unit circle.

so let's find both co ordinates of this point.

take the equation of the circle: x^2 + y^2 = 1 and the equation of the line y = A. turns out, the co ordinate is (A, sqrt(1-A^2))

now to find how long is that arc between (A, sqrt(1-A^2)) and (1,0) along the unit circle:

simply take the arctan(A/sqrt(1-A^2))) and you're done.

note, this method only works for the first quadrant, but making the rest work shouldnt be too hard.

Turing:

function arcsind (r : real) : real     result arctand (r / sqrt (1 - r ** 2)) end arcsind

[Delos]

Yes dodge, yes I am. . Ah well, I enjoyed the proof anyway, so it was worth it. But yes, do what dodge says, he knows more maths than I do.

[Phonon]

NikG wrote:

I'm just wondering... what exactly is arcsin even necessary for anyways?
I mean if you're just looking for the angle in between 2 lines, arctand is more than sufficient.

I am writing a program for x-ray crystallography. In order to find theta from bragg's law, I need to use arcsin. There's simply no other way I can do it, as far as I see, because:

sin (theta) = (n * radiation wavelength)/2*d(hkl).

Thus, knowing n, the radiation wavelength and d(hkl), I am using that information to find theta.

[Phonon]

Anyway, I got it to work. Thanks very much for the help!

[Andy]

of course you got it to work.. i gave you the exact code