Elliptical Path

[whoareyou]

I'm trying to have a basic circle follow in a circular path around the console window. However, the console window isn't a perfect square, so an elliptical path makes more sense. Before I can implement the PATH, I need to first understand how to draw an actual ellipse.

I'm trying to follow the formulas found on the Wikipedia site for an Ellipse:


Link: http://en.wikipedia.org/wiki/Ellipse#General_parametric_form

When I implemented this in my Java program, it produced this image:


This path, draw in the black, goes off of the console window, and I'm trying to make the x and y coordinates so that I can use it with a different object (perhaps a rectangle following an elliptical path across the console window). I want the path to look like the ellipse in RED, but everything I do doesn't seem to work. Any suggestions?

code:

// The "MoveCircle" class. import java.awt.*; import hsa.Console; public class MoveCircle {     static Console c;           // The output console     public static void main (String[] args) throws InterruptedException     {         c = new Console ();         int x, y, width, height, xCenter, yCenter;         x = c.maxx () / 2;         y = c.maxy () / 2;         width = 50;         height = 50;         xCenter = width / 2;         yCenter = height / 2;         for (int i = 0 ; i <= 360 ; i++)         {             x = (int) Math.round ((c.maxx () / 2) + (c.maxx () / 2 - xCenter) * (Math.cos (Math.toRadians (i))) * (Math.cos (Math.toRadians (90))) - (c.maxy () / 2 - yCenter) * (Math.sin (Math.toRadians (i))) * (Math.sin (Math.toRadians (90))));             y = (int) Math.round ((c.maxy () / 2) + (c.maxx () / 2 - xCenter) * (Math.cos (Math.toRadians (i))) * (Math.sin (Math.toRadians (90))) + (c.maxy () / 2 - yCenter) * (Math.sin (Math.toRadians (i))) * (Math.cos (Math.toRadians (90))));             c.fillOval (x - xCenter, y - yCenter, width, height);         }         c.setColor (Color.red);         c.drawOval (0, 0, c.maxx (), c.maxy ());     } // main method } // MoveCircle class

[whoareyou]

Never mind, I figured out the problem, although I don't know why it worked ...

What do "a" and "b" represent in the equation? They had to be switched to make the right shape? I though "a" was the major axis, which would've been the c.maxx() and "b" would be the c.maxy(). I'm confused.

[Raknarg]

My guess would be the radius of the ellipse. (a for x radius, b for y radius)

[Zren]

Ellipses are basically just squished circles. A circle uses:

x = cos(ang) // -1 .. 1
y = sin(ang) // -1 .. 1

Normally we scale both variables by the same amount to retain a circle. For an ellipse, just change it to xRadius and yRadius.

Circle:
x = radius * cos(ang)
y = radius * sin(ang)

Ellipse:
x = xRadius * cos(ang)
y = yRadius * sin(ang)

The rest is just necessary translation.

I have no idea what that formula does however.

Edit: Okay I may be pulling a lot of shit out of my ass due to my lack of education in this (matrixes and polar), but I think the formulas you posted combine itself with the rotation matrix. It also might be using polar grid due to there only being t and not another x+y. Bah. One formula tends to have a shitton of history. You need to walk backwards and learn all the parts of it first, then put it together.

Why I think it's rotation.
[url]http://en.wikipedia.org/wiki/Rotation_(mathematics)[/url] <-- I hate you too compsci

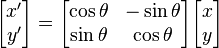
code:

[ x' ] = [ cos(ang),  -sin(ang) ][ cos(t) ] [ y' ]   [ sin(ang),   cos(ang) ][ sin(t) ] x' = cos(t)cos(ang) - sin(t)sin(ang) y' = cos(t)sin(ang) + sin(t)cos(ang) Add in the xRadius and yRadius scaling: [ x' ] = [ cos(ang),  -sin(ang) ][ xRadius*cos(t) ] [ y' ]   [ sin(ang),   cos(ang) ][ yRadius*sin(t) ] x' = xRadius*cos(t)cos(ang) - yRadius*sin(t)sin(ang) y' = xRadius*cos(t)sin(ang) + yRadius*sin(t)cos(ang) Translation to shift it so it doesn't center on a corner point. x = xRadius + xRadius*cos(t)cos(ang) - yRadius*sin(t)sin(ang) y = yRadius + xRadius*cos(t)sin(ang) + yRadius*sin(t)cos(ang)

So basically it's:

code:

ovalRotation = ... for pointAngle in range(2pi):     x = xRadius + xRadius*cos(pointAngle)cos(ovalRotation) - yRadius*sin(pointAngle)sin(ovalRotation)     y = yRadius + xRadius*cos(pointAngle)sin(ovalRotation) + yRadius*sin(pointAngle)cos(ovalRotation)

[Dreadnought]

The value 'a' is in fact the major axis of the ellipse and 'b' would be the axis perpendicular to the major axis. The reason you had to swap their values to obtain the proper shape is, as Zren explained, because you have rotated your ellipse 90 degrees, effectively placing the major axis along the y axis.

[whoareyou]

Thanks very much Zren and Dreadnought! I understand my mistake now!