predicate logic proofs
| Author |
Message |
Fonzie
|
 Posted: Sun Oct 05, 2008 3:40 pm Post subject: predicate logic proofs Posted: Sun Oct 05, 2008 3:40 pm Post subject: predicate logic proofs |
|
|
I have a question on my assignment that I'm having a great deal of trouble with.
In this question we will
consider a simplified model of the ?People you may know? application in Facebook. The
basic idea is that if two people have a common friend, then they may know each other. We
will also take into account the fact in Facebook the relation ?friend? is symmetric, that is,
if X is a friend of Y , then Y is a friend of X.
Thus, as a problem description P, we have the following two predicate logic sentences:
8X8Y [(9Z(friend(X, Z) ^ friend(Z, Y ))) $ may know(X, Y )]
8X8Y [friend(X, Y ) ! friend(Y,X)]
Our goal is to show, using resolution refutation, that the following sentence g is implied by P:
8X8Y [may know(X, Y ) ! may know(Y,X)].
8 = universal quantifier
9 = existential quantifier
$ = biconditional
! = implication
I have derived the following clauses (this is for a logical programming class):
c1: may_know(X,Y) :- friend(X,T), friend(T,Y)
c2: friend(X,f(X,Y,T)) :- may_know(X,Y)
c3: friend(f(X,Y,T),Y) :- may_know(X,Y)
c4: friend(Y,X) :- friend(X,Y)
c5: may_know(d,e) :-
c6: :- may_know(e,d)
I've attempted linear refutation which won't work. The question goes on to advise that you prove g from p "using your normal, mathematical, reasoning. Then, try to re-create the steps of your proof using resolution on your clauses." This is where I'm stuck, I'm not sure how I can prove g from p using either my clauses or my ordinary mathematical reasoning. Any help with this would be greatly appreciated. |
|
|
|
|
 |
Sponsor
Sponsor


|
|
 |
Clayton

|
 Posted: Sun Oct 05, 2008 3:46 pm Post subject: RE:predicate logic proofs Posted: Sun Oct 05, 2008 3:46 pm Post subject: RE:predicate logic proofs |
|
|
If I wasn't having so much trouble reading the math, I might be able to help you out a bit better, I think the LaTeX tags work...
 |
|
|
|
|
 |
Fonzie
|
 Posted: Sun Oct 05, 2008 4:07 pm Post subject: Re: predicate logic proofs Posted: Sun Oct 05, 2008 4:07 pm Post subject: Re: predicate logic proofs |
|
|
revised problem
p:
 X X Y [( Y [(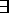 Z(friend(X, Z) ^ friend(Z, Y ))) Z(friend(X, Z) ^ friend(Z, Y )))  may know(X, Y )] may know(X, Y )]
 X X Y [friend(X, Y ) Y [friend(X, Y ) 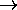 friend(Y,X)] friend(Y,X)]
g:
 X X Y [may know(X, Y ) Y [may know(X, Y ) 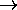 may know(Y,X)] may know(Y,X)]
sorry, took me a bit to figure out how to get the pictures in there. |
|
|
|
|
 |
|
|

