Binary, Logic IC's, Bits, Bytes, Circuitry and Chips!
| Author |
Message |
GreatPumpkin
|
 Posted: Sat Feb 22, 2014 6:56 pm Post subject: Binary, Logic IC's, Bits, Bytes, Circuitry and Chips! Posted: Sat Feb 22, 2014 6:56 pm Post subject: Binary, Logic IC's, Bits, Bytes, Circuitry and Chips! |
|
|
I'm somewhat surprised to see a lack of talk about logic IC's, after all they were the technology that lead to the computers we use to program on. I thought there'd be an entire section dedicated to those fun little chunks of silicone. For those of you who don't know what logic IC's are or how computers function, here's some insight in my words:
The Binary Number System
Binary is a number system much like our common (decimal) base 10 system we learnt in grade 3 but can hardly remember the vocabulary for  . In base 10 each column can hold 0-9 (10 numbers). Binary is a base 2 system. Each column can hold either a 0 or a 1 (2 numbers). Instead of a 1's column, 10's column and 100's column binary uses a 1's column, 2's column, 4's column, 8's column, 16's column continuing to double indefinitely. This may be hard to understand so I'll elaborate. . In base 10 each column can hold 0-9 (10 numbers). Binary is a base 2 system. Each column can hold either a 0 or a 1 (2 numbers). Instead of a 1's column, 10's column and 100's column binary uses a 1's column, 2's column, 4's column, 8's column, 16's column continuing to double indefinitely. This may be hard to understand so I'll elaborate.
Lets look at the number 3: in base 10, the number 3 takes up only the ones column, because it does not go past 9. In base 2 however it takes up two columns.
The rightmost number is the one's column, although it's the same as the base 10's 1's column keep in mind the confusion that can be caused when teaching a child 2 * 2 = 4 as an introduction to multiplication.. A single 1's column. can represent the numbers 0 and 1. If we were to count up to 2, it needs to be represented as a 10, with a second column. This is because each column only has space to represent 0 and 1, not 0-9 like our decimal system. So much like when we count from 9 to 10, we need another column for the excess numbers. Imagine counting from 0 to 4, in a system were a number 2/3/4 doesn't exist but a value of 2/3/4 does exist.
0 + (0)
1 = (1)
1 (1)
Pretty straight forward, there is no carry over.
01 + (1)
01 = (1)
10 (2)
The two 1's in the first column add up and carry over to the second column.
When counting from 2 (10) to 3 (11) however, we do not need another column. This is because the first column is 0.
10 + (2)
01 = (1)
11 (3)
and one more
11 + (3)
01 = (1)
100 (4)
Another name for the columns are "Bits", short for Binary Digits.
0/1 are 1 bit numbers, 2/3 or 10/11 are two bit numbers, 4 - 7 are 3 bit numbers and 8 - 15 are 4 bit numbers.
0000 = 0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
0101 = 5
0110 = 6
0111 = 7
1000 = 8
1001 = 9
1010 = 10
1011 = 11
1100 = 12
1101 = 13
1110 = 14
1111 = 15
100110 = 38 figure that one out
Now you should have a basic understanding of the Binary number system! If not this page http://computer.howstuffworks.com/bytes.htm and this page http://php.about.com/od/programingglossary/qt/binary.htm have great explanations, better than mine.
A Computers Relation to Binary
Quote:
A bit is the basic unit of information in computing and digital communications. A bit can have only one of two values, and may therefore be physically implemented with a two-state device. The most common representation of these values are 0and1. The term bit is a portmanteau of binary digit.
The two values can also be interpreted as logical values (true/false, yes/no), algebraic signs (+/−), activation states (on/off), or any other two-valued attribute.
We've all heard that computers think in 1's and 0's, but it's not something you can really understand without knowing about binary. Hopefully you can begin to understand it now. As mentioned in the quote above, binary bits can be represented as on/off, as in the positive or negative charges in wires and silicon chips. These frequently changing groups of on/off charges inside your computer's chips are what causes it's calculations.
A group of 8 bits is known as a byte, 1024 as a kilobyte, the rest should be common knowledge for us all.
More information on Bits and Bytes here: http://computer.howstuffworks.com/bytes.htm
Logic Gates and IC's
Logic integrated circuit's are building blocks of all digital computing. They're made up transistors, which are essentially a semi-conductive straight wire with a third lead, the wire only allows power to flow through when the third lead is powered. Like a relay or digitally activated light switch. Logic IC's are combinations of transistors which allow for certain combinations of logic gates: and, or, not along with xor, nand, nor, xnor, which are larger combinations of the first three. Here is a visual representation of AND gate and chip:

This is a AND chip.
Along the bottom are leads 1 - 7, along the top are leads 8 - 14. 7 must be connected to ground (0) while 14 must be connected to power (1), these leads power the chip. The chips are always to be read from the bottom to the top with the cut-out or dent on the left side, text upright, as pictured in the image.
This is the truth table for an AND gate. Truth tables are pretty much calculation graphs, which include the inputs on the left side and all possible outputs on the right side of a single chips or set of chips. The schematic symbol is included, this is what is used when drawing out designs to be copied and recreated.

The output is only true when both inputs A and B are true. Remember, true/false = on/off = +/- = powered/grounded.
Now we can see that the 7408 chip pictured has 4 and gates within it. Alone it's not to useful, we can hook an led or motor up to the output (Q) of the first AND gate (pin 3) and when both inputs A and B (pins 1/2) are true, powered, or not grounded it will activate, fantastic, a light switch could do the same.
How Bit's and Bytes can be Physically Created and Designed to Interact with Each Tther
It's when we begin to combine chips with each other that we really start to get some useful. By combining an XOR gate or exclusive OR gate:
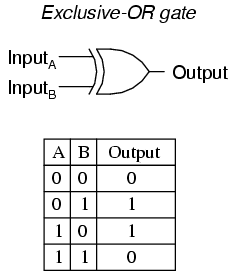
with the AND gate like so:

And you have a calculator! Well somewhat, it's called a half adder.. If you connect the SUM and CARRY to there own LED's, then leave A and B off/false/negative, neither LED will be turned on. If you have either A or B, but not both true, then the first LED will turn on. As soon as both A and B are true, the 1st LED will turn off and the 2nd will turn on. This perfectly resembles the operation of 01 + 01 = 10, as shown in the truth table! The inputs and outputs can be considered bits. Each input is a single bit, when both bits are added, you get the 2-bit number 2. By connecting the CARRY of the half adder to the A input of another half adder, and connect the SUMS with an OR gate, we get a full adder. Now we can count from the 1-bit number 0 to the 2-bit number 3, for a total of four numbers.


http://electronics.howstuffworks.com/transistor.htm More on transistors.
http://computer.howstuffworks.com/boolean2.htm More on Boolean Logic Gates.
http://whatis.techtarget.com/definition/logic-gate-AND-OR-XOR-NOT-NAND-NOR-and-XNOR More on Boolean Logic Gates.
Resources for Those Interested in Circuitry
http://en.wikipedia.org/wiki/List_of_7400_series_integrated_circuits List of 7400 chips
http://mrkurz.ca/1TEJ3.html My teachers webpage from my last years class (Will likely be reset in September) It is full of projects for Turing, IC circuitry, and assembly language.
http://cpuville.com/ A much simpler homemade CPU.
http://members.iinet.net.au/~daveb/simplex/ringhome.html Webpage of homemade computers from logic IC's. The magic-1 is capable of internet access, it uses an entirely homemade architecture and operating system.
http://logic.ly/ A powerful logic gate simulator.
http://www.kolls.net/gatesim/ Another logic simulator inspired by Logic.ly however this one is free and open source.
http://www.ebay.com/itm/ELECTRONIC-PROJECT-STARTER-KIT-B-BREADBOARD-CAPACITOR-LED-RESISTOR-WIRES-/230881393379 A beginner kit for breadboard circuitry.
Projects to look up, counters, Flip Flops, Latch's, Registers, Multiplexor's and Decoders.
I hope this post will inspire the compsci community to develop an interest in circuitry, as it is essentially a form of programming. I'm sure there are other people who are currently or have worked on circuitry projects, even though it would likely be one of the least active sections, I think a section on circuitry is well needed!
Last year I began creating a robot which could be programmed to turn in a series of pre specified directions when it got near a wall. It worked great except for the lack of a Schmitt Trigger, I had ordered the one to avoid noise in buttons, not infrared light . It was made entirely from 7400-series. I haven't touched IC's since then, but I pulled my old falling apart robot out of my last years project box this week, and got thinking about it again.
This year I'm either going to dedicate my class time into creating a simple computer from 7400 series chips, with my own assembly language, or finish my civilization like video game.
I've surpassed my teachers knowledge about circuitry and I believe about Turing too. I'd be happy to try to answer any questions ya'll might have. If anybody spots any misinformation or has anything to add, please let me know ASAP.
Let the discussion's start to roll? |
|
|
|
|
 |
Sponsor
Sponsor


|
|
 |
GreatPumpkin
|
 Posted: Mon Mar 03, 2014 1:34 pm Post subject: RE:Binary, Logic IC\'s, Bits, Bytes, Circuitry and Chips! Posted: Mon Mar 03, 2014 1:34 pm Post subject: RE:Binary, Logic IC\'s, Bits, Bytes, Circuitry and Chips! |
|
|
| No interest whatsoever ? |
|
|
|
|
 |
[Gandalf]

|
 Posted: Wed Mar 05, 2014 7:38 pm Post subject: Re: Binary, Logic IC's, Bits, Bytes, Circuitry and Chips! Posted: Wed Mar 05, 2014 7:38 pm Post subject: Re: Binary, Logic IC's, Bits, Bytes, Circuitry and Chips! |
|
|
| Pretty good writeup! In my Computer Organization course we designed and implemented a simple CPU using such logic gates - that's as far as I've delved into the topic. It's very interesting stuff and a relatively bottom up approach compared to most of CS which is often top down. However, because it's more of a computer engineering / low level thing, most CS people aren't as involved / interested in this stuff. |
|
|
|
|
 |
bl0ckeduser
|
 Posted: Sat Mar 08, 2014 5:27 pm Post subject: Re: Binary, Logic IC's, Bits, Bytes, Circuitry and Chips! Posted: Sat Mar 08, 2014 5:27 pm Post subject: Re: Binary, Logic IC's, Bits, Bytes, Circuitry and Chips! |
|
|
I have a course like this at school and they make us use a gates simulator called LOGISIM which is pretty nice.
At my old school I had a similar course and the prof linked to a free textbook called "Lessons in Electric Circuits", http://www.ibiblio.org/kuphaldt/electricCircuits/Digital/index.html.
It covers more advanced stuff like multiplexers and Karnaugh maps. |
|
|
|
|
 |
|
|

