Help evaluating this in closed form? (with binomial coefficients)

[DtY]

I've come across this problem in a math book, and I can't figure it out.



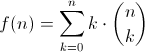
This is pretty early in the book, and it hasn't gotten into any sort of summation analysis (in fact it hasn't even introduced sigma notation--in the book it shows the sum with an ellipsis), so the instructions are to evaluate it for a few small values and look for a pattern, then prove it using induction. However, I could not find any patterns, so I tried playing around with it using what I do know about sums. The book also asked to try to explain it using combinatorial reasoning, but I can't think of what it could mean (although, in a dream I had last night, someone told me that it was representing all the subsets of letters in either upper or lower case (this sounds weird, but when you hear something in a dream it readily makes a lot more sense, basically all the subsets of k elements where each element could be one of two values), but after I woke up and looked at it again this would be 2**k. It seems to me that this would represent the number of rotations (like ABC, CAB, BCA), but I'm not sure if that helps.

Two observations I did make though:

- Each binomial coefficient is being multiplied by a number that is at least one except when k=0, so if I replace it with a one and subtract n choose 0 it will be less than or equal to the original
- Each binomial coefficient is being multiplied by a number that is less than or equal to n, so if I replace it with n it will be greater than or equal to the original.

These are both easily evaluated in a closed form:




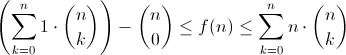
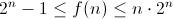
And some calculations I did earlier today on these three functions: (starting at n=0)

code:

0 <=          0 <=          0          1 <=          1 <=          1          3 <=          4 <=          8          7 <=         12 <=         36         15 <=         32 <=        128         31 <=         80 <=        400         63 <=        192 <=       1152        127 <=        448 <=       3136        255 <=       1024 <=       8192        511 <=       2304 <=      20736       1023 <=       5120 <=      51200       2047 <=      11264 <=     123904       4095 <=      24576 <=     294912       8191 <=      53248 <=     692224      16383 <=     114688 <=    1605632      32767 <=     245760 <=    3686400      65535 <=     524288 <=    8388608     131071 <=    1114112 <=   18939904     262143 <=    2359296 <=   42467328     524287 <=    4980736 <=   94633984    1048575 <=   10485760 <=  209715200    2097151 <=   22020096 <=  462422016

I don't want a solution, but some pointers would be great, thanks.

e; Another observation I made was that all the numbers I looked at closely (up to n=5) were mostly prime factored into a bunch of twos and just one other factor, in fact a bunch of them had n factors of two and one factor of either three or five, but didn't look like a conclusive pattern.
e; fixed the formulae.

[DemonWasp]

Take a good, long look at Pascal's Triangle. Specifically, look at the rows in that triangle. Even more specifically, consider their sum.

[DtY]

DemonWasp @ Thu Jan 27, 2011 10:30 pm wrote:

Take a good, long look at Pascal's Triangle. Specifically, look at the rows in that triangle. Even more specifically, consider their sum.

I know that the sums are powers of two, but I need to multiply each by k, are you sure this is related?

There is no general way to evaluate the sum of two terms that are both dependant on the index variable, is there? (the way you can split up addition, or factor out a term that is not dependant on the index).

[Brightguy]

Here's a hint (of hopefully the right level):


Darn it, why did LaTeX support have to break?

[DtY]

Thank you! I can't believe I didn't notice that, after a few minutes of convincing myself that was true, I got the equation pretty quickly. I can't believe how close I came (my upper bound looks very similar to it, and I should have seen the pattern once I'd prime factored the terms).

(spoiler alert) For anyone who's interested, the closed form equation is n*2**(n-1)

And now, I'm still not sure about the combinatorial meaning of this, any hints?

[Brightguy]

You've seen the combinatorial reasoning for the unscaled sum, right? (The number of binary strings of length n.) Well, consider the total number of 1s in the binary strings of length n.

[DtY]

Brightguy @ Fri Jan 28, 2011 1:33 am wrote:

You've seen the combinatorial reasoning for the unscaled sum, right? (The number of binary strings of length n.) Well, consider the total number of 1s in the binary strings of length n.

Okay, I've been thinking about this for the last week, and I think I get it now, kinda.

So, there are 2**n binary strings of length n, right? Which would be the sum of all n pick 0 + n pick one + ... + n pick n, because it could have zero ones, one one, two ones... or n ones. And then with this, in the case that there are no ones, there is a total of zero ones, and then if there is one one there will be n ones, because there is a total of n possibilities, each having one one, and then so on.

Is that all right? Is that all this means, or is it useful in some way that I'm not seeing?

[Brightguy]

That's correct. And this combinatorial perspective helps you evaluate the sum because there is a more straightforward way of counting the total number of 1s in the binary strings of length n.

I can be more direct, but if you're anything like me you enjoy thinking about this.