Using information to solve problems [part 1]

[MihaiG]

So the basis of good programming is the ability to make your computer to your work for you.

For example one problem often given to programmers in more intermediate/advanced high school classes is to design a program that outputs a number of rows from Pascal's Triangle. Now without reading to much into the history of pascals triangle we look at the image listed below and try to infer the pattern.



now we can see the sides always stay the same ( they are always 1) and that the next term in a sequence is the additive value of the two numbers above it and so on.
this explains why the sides are always one, since they are 0 + 1.
There are many properties that will help us define notation used for pascals triangle. The grid can be subsequently arranged like so:

Quote:

1 "0"
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

the first row will always be reffered to as row 0 this is defined by the second number in row 0 which has been put to show that the second number in each row (or second last) always give us the row number of that subsequent row.

so the first idea that would jump into the average programmers head would be to use lots of arrays and variables and loops to add up the previous two nubmers in the sequence to give us the next number. This would require us to have maybe two flexible arrays that we can add items to and then parse through them to find the previous values.

So whats is the point of this topic well here we go.

Chances are someone has already done what you have and has done it better (probably with thsi tutorial as well ). So before any code is written the best idea is to research the assignment so yuo understand it perfectly (that means if i break into your house and wake you up and ask what pascal's triangle is you can tell me).

So lets head over to the wiki page(note wikipedia is not always the best, but it will work most of the time)



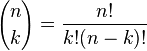
is one of the first images we see what does it mean
well it is used in probability to calculate the combination of a certain group of objects where the order does not matter.
back to pascal's triangle though

so it says n! / (n-k)!*k!

so what do these arbitery constants mean well heres the deal.
some guy found that if you put n as your row number and k as your column number hey, you get that specific term in your calculator what a suprise!

Quote:

so what are you saying mihai? we can calculate every term using this simple formula and not have to use complex arrays?

yup thats it!

so our first step if were to write this in turing would be to write a function that calculates factorials

code:

function fact (num : int) : int     var test : int := 1     if num = 0 then         result 1     else         for i : 1 .. num             test := test * i         end for         result test     end if end fact

so we just have a local variable which we just multiply to itself in a for loop, note we need the special case where the input is 0 to be equal to 1

so now all we have to do is setup a bunch of for loops that will just output that data for us
here goes

code:

for i : 0 .. num - 1     for j : 0 .. (i)         put (fact (i) / (fact (i - j) * fact (j))), "   " ..     end for     put "" end for

now why did i subtract 1 from num, this is because our first row is called row 0 and if we didn't we would be outputting two rows instead of one
the space and the two periods allow for spacing and for trailing of the output on the same line

so now if we put these two pieces of code together we get:

code:

function fact (num : int) : int     var test : int := 1     if num = 0 then         result 1     else         for i : 1 .. num             test := test * i         end for         result test     end if end fact var num : int get num for i : 0 .. num - 1     for j : 0 .. (i)         put (fact (i) / (fact (i - j) * fact (j))), "   " ..     end for     put "" end for

so using this i made a calculator for pascal's triangle in less than 20 lines of code huzzah
now to see if it works
i put in 13 and i get

Quote:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1

woohoo
it works

So,
researching a topic before hand especially something that fairly challenging will help because there should be more than enough information available to make everything easier for you.

So next week (or in two weeks), ill post a tutorial on converting algebraic expressions such as infix to prefix and postfix, which is how machines evaluate expressions, yay!


EDIT**
Note,if you try 14 it will break, since were evaluating each factorial separate this is inefficient you can do this by simplifying out stuff beforehand, ill post a procedure that does that either later on today or tommorow

[r691175002]

IMO Pascals triangle is a bad example because really, arrays are the better way to go here. Limiting your program to take a maximum of 13 is pretty brutal, as is calculating three factorials for each number.

You could implement a recursive solution that avoids arrays and executes faster than your current program, however at that point you might as well tack on an array for memoization, or just implement a dynamic solution which comes back to arrays again.

[Carey]

See the demo I made. It's HERE