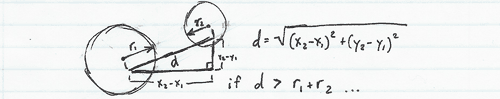Computer Science Canada

Something Interesting Regarding Circle collision
Author:  Dragon20942 [ Wed Feb 23, 2011 9:53 pm ]
Post subject:  Something Interesting Regarding Circle collision
What is it you are trying to achieve?
So I was wondering if we use the Pythagorean theorem to find the exact pixels of a circle's circumference, or if there is an easier way. From my current Gr. 10 math, it is suggested that we must substitute every value of x to get y (or vice versa) using the radius as the hypotenuse. However, this would create some issues concerning the amount of computing required to run a for-loop running as many times as there are pixels in the radius.
Author:  Tony [ Wed Feb 23, 2011 10:04 pm ]
Post subject:  RE:Something Interesting Regarding Circle collision
Checking all the pixels is not guaranteed to work. The trivial counter-example is where one circle is completely inside a bigger circle. More interesting edgecases are those where pixels round in such a way that they don't end up in the same spot.

Try drawing some diagrams to get other ideas; http://compsci.ca/blog/super-paper-programming/

Posted Image, might have been reduced in size. Click Image to view fullscreen.
Author:  Dragon20942 [ Wed Feb 23, 2011 10:09 pm ]
Post subject:  RE:Something Interesting Regarding Circle collision
The fact that you use the centers of both circles instead of just the center of one circle and the end of its radius provides a new concept for me. Id better think that out before coding. Thanks!
Author:  Insectoid [ Thu Feb 24, 2011 12:01 am ]
Post subject:  RE:Something Interesting Regarding Circle collision
There are a number of tutorials on this from very basic concepts to advanced collision correction scattered around the forums. Have a look.
Author:  mirhagk [ Thu Feb 24, 2011 8:26 am ]
Post subject:  RE:Something Interesting Regarding Circle collision
Cicle collision is the simplest, and arguably the most important collision detection.

Almost any shape can be rougly estimated with a circle, allowing you to quickly check to see if something could potentially intersect something else without a full collision detection.

Also it's a matter of how far something is from another thing, every mission objective that involves getting to a specific point uses circle collision detection to see if your close enough.


Oh and a quick tip, the mathematical algorithm is
code:

d=sqrt((x2-x1)^2+(y2-y1)^2)
if (d<=r1+r2)
   print (They hit)

This is the proper way to do it, but a suggested hack is to drop the square root sign, and then just square (r1+r2). The cost to multiply two numbers is a lot cheaper than the cost of doing a square root.

code:

d=(x2-x1)^2+(y2-y1)^2
if (d<=(r1+r2)^2)
   print (They hit)
Author:  DemonWasp [ Thu Feb 24, 2011 8:28 am ]
Post subject:  RE:Something Interesting Regarding Circle collision
Long story short: two circles (or spheres, or hyperspheres) are intersecting (have collided) if the distance between their centres is less than the sum of their radii.
Author:  Dragon20942 [ Fri Feb 25, 2011 6:00 pm ]
Post subject:  RE:Something Interesting Regarding Circle collision
Great! I got:
Turing:

var rad1 := 25 %radius of first circle (red)
var rad2 := 25 %radius of second circle (green)
var circleX := Rand.Int (rad1, maxx - rad1)%red
var circleY := Rand.Int (rad1, maxy - rad1)
var circle2X := Rand.Int (rad2, maxx - rad2)%green
var circle2Y := Rand.Int (rad2, maxy - rad2)
var circleColour := red
var circleColour2 := green
var circleXVel : int
var circle2XVel : int
var circleYVel : int
var circle2YVel : int

loop
    circleXVel := Rand.Int (-3, 3)
    circle2XVel := Rand.Int (-1, 1)
    circleYVel := Rand.Int (-3, 3)
    circle2YVel := Rand.Int (-1, 1)
    exit when circleXVel not= 0 and circle2XVel not= 0 and circleYVel not= 0 and circle2YVel not= 0
end loop

var xDiff, yDiff, cDiff : real         %cDiff is the distance between the two centers of the circles (hypotenuse)

View.Set ("offscreenonly")

loop

    circleX += circleXVel
    circleY += circleYVel
    circle2X += circle2XVel
    circle2Y += circle2YVel


    if circleX < rad1 then
        circleXVel := circleXVel * (-1)
    elsif circleX > (maxx - rad1) then
        circleXVel := circleXVel * (-1)
    end if
    if circleY < rad1 then
        circleYVel := circleYVel * (-1)
    elsif circleY > (maxy - rad1) then
        circleYVel := circleYVel * (-1)
    end if

    if circle2X < rad2 then
        circle2XVel := circle2XVel * (-1)
    elsif circle2X > (maxx - rad2) then
        circle2XVel := circle2XVel * (-1)
    end if
    if circle2Y < rad2 then
        circle2YVel := circle2YVel * (-1)
    elsif circle2Y > (maxy - rad2) then
        circle2YVel := circle2YVel * (-1)
    end if

    xDiff := (circleX - circle2X)
    yDiff := (circleY - circle2Y)
    cDiff := (xDiff ** 2 + yDiff ** 2) ** (1 / 2)

    put "Pixels between midpoints: ",cDiff

    if cDiff < rad1 + rad2 then %if the hypotenuse is less than the combined radii, then
        circleColour := blue
        circleColour2 := blue
        delay (100)
    else
        circleColour := red
        circleColour2 := green
    end if

    drawfilloval (circleX, circleY, rad1, rad1, circleColour) %green
    drawfilloval (circle2X, circle2Y, rad2, rad2, circleColour2) %red

    View.Update
    delay (5)
    cls
end loop


Ok so I go and make up some code before realizing that you guys already posted it...

:


You can syndicate this boards posts using the file backend.php or view the topic map using sitemap.php.

Terms of Use | Privacy Policy