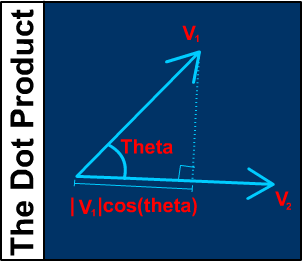
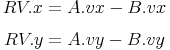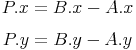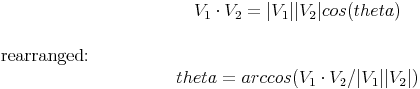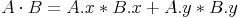Perfect Circle-Circle Collision Detection
Circular collision detection is a fundamental concept in many types of games. Although there are many different
methods one can use to detect a collision between two circles, the method I am about to describe allows for
accurate collision detection even when the circles are moving at high speeds. Additionally, this method will
allow your program to draw every collision that occurs (if you so wish).
The simplest method to detect a collision is to check if the circles are overlapping. This can be done by
directly applying the Pythagorean Theorem. If The distance between the centers of the two circles is less than or
equal to the sum of the radii of the circles, then a collision has occured. The square root in the distance
formula is unnecessary because the inequality will still hold if we square both sides. Removing the square root
can increase your collision detection especially if you are checking for many collisions.
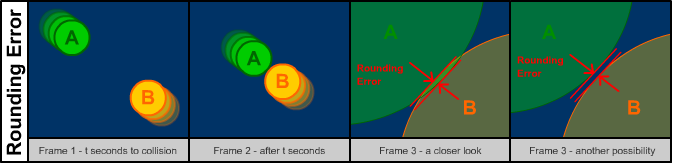
This method can be satisfactory for many applications but in many cases a more accurate method will be needed. For
instance, what if you require your collision detection algorithm to detect the collisions exactly when they
occur, ie. such that no overlapping occurs? Also if the circles are moving fast enough, this method might not
catch the collision at all! For example, if two circles are close together and moving very quickly towards each
other, in the next frame they could already be past each other. No collision is detected because the collision
occurs in between frames. This problem is not uncommon and is one of the challenges one must overcome when
creating a pool game.
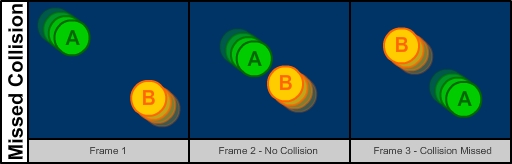
Figure 1 - Collision Between Frames
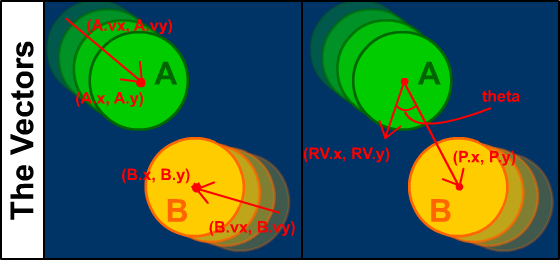
In order to overcome this problem, you need to use a little math. First lets describe the position of a pool ball
that is in motion with no friction acting on it (we will add this later). So the ball will have a certain position
(x, y), and a constant velocity (vy, vy). The ball's new position (x', y'), can be described like so:
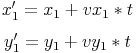
Since we will be dealing with more than one ball we use subscripts to describe which ball we are talking about.
The new position is the position of the ball after t time. In our case the unit for t is frames, so if we set
t = 1, then the new position is where the ball will be in the next frame of animation. With these equations, we
can now write a distance equation which, tells us the distance between the centers of the balls. This equation can
be written like so:
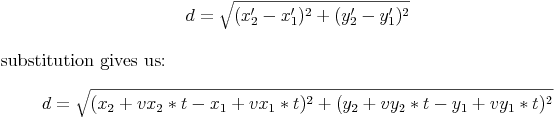
Now that we have our distance equation, we can figure out exactly when a collision occurs. All we have to do is
isolate the variable t. This is easier said than done. Using a math program like mathematica or matlab or maple,
you get the equation:
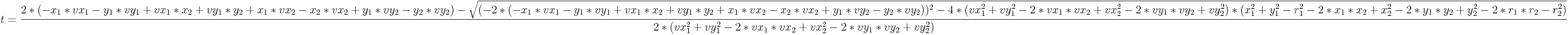
Note that since there is a square root in our equation, t may take on two values, one value, or no values at all
and we need to take this into account when we are programming our solution. No solution occurs when there wont be
a collision between the balls, one solution occurs when the balls just skim each other, and two solutions occur
when the balls collide normally. The first solution tells us when the balls initially collide and the second
solution tells us when the balls will touch if they were allowed to pass through each other. Note: A collision in
this case is defined as the balls just touching. If the balls are overlapping, this is not considered a collision.
(this scenerio should never occur anyways)
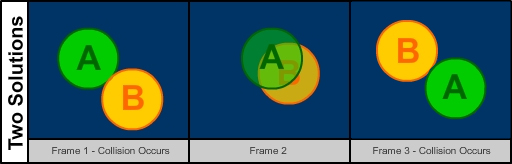
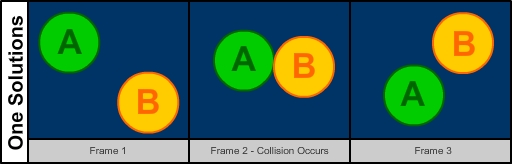
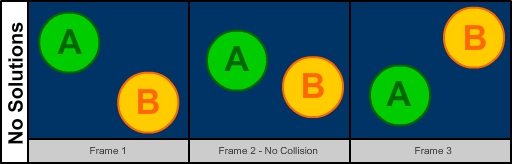
Figure 2 - Different Solution Types
Now that we have our formula for time, we can start writing some code. Lets start with writing some code which we
can use to test our collision detection:
| Turing: |
View.Set ("offscreenonly")
type BallData : record x, y, vx, vy, r : real end record /* The amount of delay between frames */ const DELAY := 50 /* We anticipate many balls so we create an array */ var balls : array 1 .. 2 of BallData /* Stores the amount of time untill a collision occurs */ var t : real balls (1).x := 200 balls (1).y := 150 balls (1).vx := 4 balls (1).vy := 4 balls (1).r := 20 balls (2).x := 300 balls (2).y := 250 balls (2).vx := -4 balls (2).vy := -2 balls (2).r := 20 /* Returns the amount of frames untill a collision will occur */ fcn timeToCollision : real var t : real := maxint result t end timeToCollision /* Draws all the balls to the screen */ proc drawBalls for i : 1 .. upper (balls) Draw.Oval (round (balls (i).x), round (balls (i).y), round (balls (i).r), round (balls (i).r), black) end for end drawBalls /* Updates all the balls attributes. If a collision Occures in between frames, * * the balls will be updated to the point of the collision. We return when the * * collision occurs so that we can adjust the delay in the main loop. */ fcn updateBalls : real /* We want to increment by at most one frame */ var t := min (1, timeToCollision) for i : 1 .. upper (balls) balls (i).x += balls (i).vx * t balls (i).y += balls (i).vy * t end for result t end updateBalls /* Checks if a collision has occured between any of the balls */ proc checkForCollision for i : 1 .. upper (balls) for j : i + 1 .. upper (balls) if (balls (j).x - balls (i).x) ** 2 + (balls (j).y - balls (i).y) ** 2 <= (balls (i).r + balls (j).r) ** 2 then put "Collision has occurd!" drawBalls View.Update delay (500) /* Collision reaction code should replace the above four statements. * * We will leave collision reaction for another tutorial ;) */ end if end for end for end checkForCollision /* Main animation loop */ loop drawBalls checkForCollision t := updateBalls View.Update cls /* If a collision occurs in between frames, we have to use a shorter delay * * to keep the animation speed consistent */ Time.DelaySinceLast (round (DELAY * t)) end loop |
Listing 1 - Collision Detection Test Program
This program is pretty straight forward. At this point, it is using the simple method for collision detection
mentioned earlier in this tutorial. Notice how a collision is recognized when the balls are already overlapping.
We need to update our timeToCollision function such that it will tell us exactly when the collision will occur.
Since the formula for t is quite large we will need to break it up a little. Also, we need to remember that there
are three possible types of solutions. If we get two solutions, we return the smaller one since this is when the
first collision occurs rather than the second collision that occurs if the balls were allowed to pass through
each other. If no collision occurs, we return a large value to indicate that no collision will occur any time
soon.
| Turing: |
/* Returns the amount of frames untill a collision will occur */
fcn timeToCollision : real var t : real := maxint var A, B, C, D, DISC : real /* Loop through every pair of balls and calculate when they will collide */ for i : 1 .. upper (balls) for j : i + 1 .. upper (balls) /* Breaking down the formula for t */ A := balls (i).vx ** 2 + balls (i).vy ** 2 - 2 * balls (i).vx * balls (j).vx + balls (j).vx ** 2 - 2 * balls (i).vy * balls (j).vy + balls (j).vy ** 2 B := -balls (i).x * balls (i).vx - balls (i).y * balls (i).vy + balls (i).vx * balls (j).x + balls (i).vy * balls (j).y + balls (i).x * balls (j).vx - balls (j).x * balls (j).vx + balls (i).y * balls (j).vy - balls (j).y * balls (j).vy C := balls (i).vx ** 2 + balls (i).vy ** 2 - 2 * balls (i).vx * balls (j).vx + balls (j).vx ** 2 - 2 * balls (i).vy * balls (j).vy + balls (j).vy ** 2 D := balls (i).x ** 2 + balls (i).y ** 2 - balls (i).r ** 2 - 2 * balls (i).x * balls (j).x + balls (j).x ** 2 - 2 * balls (i).y * balls (j).y + balls (j).y ** 2 - 2 * balls (i).r * balls (j).r - balls (j).r ** 2 DISC := (-2 * B) ** 2 - 4 * C * D /* If the discriminent if non negative, a collision will occur and * * we must compare the time to our current time of collision. We * * udate the time if we find a collision that has occurd earlier * * than the previous one. */ if DISC >= 0 then /* We want the smallest time */ t := min (min (t, 0.5 * (2 * B - sqrt (DISC)) / A), 0.5 * (2 * B + sqrt (DISC)) / A) end if end for end for result t end timeToCollision |
Listing 2 - Improved timeToCollision Function