Could someone please explain guide me in the right direction as to how to find the inverse of this function?

Computer Science Canada Inverse of a Function |
| Author: | whoareyou [ Wed Sep 12, 2012 9:43 pm ] |
| Post subject: | Inverse of a Function |
Could someone please explain guide me in the right direction as to how to find the inverse of this function?  |
|
| Author: | Aange10 [ Thu Sep 13, 2012 8:09 am ] |
| Post subject: | RE:Inverse of a Function |
if y = 1/2 (e^x - e^-x) then the inverse is switching the x and y. x = 1/2 (e^y - e^-y). |
|
| Author: | whoareyou [ Thu Sep 13, 2012 8:10 am ] |
| Post subject: | RE:Inverse of a Function |
Yeah I got that much, but how would you then isolate for y? |
|
| Author: | Zren [ Thu Sep 13, 2012 1:33 pm ] |
| Post subject: | RE:Inverse of a Function |
Found this. No idea how they got from a -> b though. 
Edit: Ah. Totally forgot about what negative exponents actually represent. 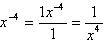
So essentially they write it as: (1/2)(e^x - (1/e^x)) Which they factor out: (1/2)(1/e^x)((e^x/(1/e^x)) - 1) (1/2)(1/e^x)((e^x * e^x) - 1) (1/2)(1/e^x)(e^2x - 1) |
|
| Author: | bl0ckeduser [ Fri Sep 14, 2012 8:37 am ] |
| Post subject: | Re: Inverse of a Function |
I have no idea how to help you with this problem, but in light of Zren's saying the function is the same as sinh, maybe this page, which deals with the inverse of sinh, will help. http://en.wikipedia.org/wiki/Inverse_hyperbolic_function |
|
| Author: | Zren [ Fri Sep 14, 2012 11:45 am ] |
| Post subject: | RE:Inverse of a Function |
Ah. Looks like the hotlinked image is down. http://www.purplemath.com/modules/simpexpo2.htm Basically it stated that: x^-y = 1/x^y |
|