1) those type of questions follow from definition: http://en.wikipedia.org/wiki/Big_O_notation
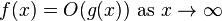
iff

finding M and x0 is sufficient.
2) count the number of computations the algorithm performs.
Computer Science Canada time complexity and Big-Oh |
| Author: | dddx [ Wed Sep 21, 2011 1:37 pm ] |
| Post subject: | time complexity and Big-Oh |
Hi guy, I am doing my assignment and found some of the questions unfamiliar. I might have missed something in the class but i couldn't find them in the notes either so i would greatly appreciate it if some one could explain the step by step solution so i can learn from it. Here are the questions: 1) Show that 2^(n+1) is O(2^n) 2) Algorithm A executes an O(log n)-time computation for each entry of an n-element array. What is the worst-case running time of Algorithm A? Thank you in advance |
|
| Author: | Tony [ Wed Sep 21, 2011 2:23 pm ] |
| Post subject: | Re: time complexity and Big-Oh |
1) those type of questions follow from definition: http://en.wikipedia.org/wiki/Big_O_notation 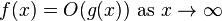
iff 
finding M and x0 is sufficient. 2) count the number of computations the algorithm performs. |
|
| Author: | Insectoid [ Wed Sep 21, 2011 3:06 pm ] |
| Post subject: | RE:time complexity and Big-Oh |
Complexity is independent of the actual number of operations. Rather, it is the rate of growth of the function that is important. The derivatives of 2^(n+1) and 2^n are equal- therefore they are the same complexity (this might not always work and might even be a very bad way to show equivalence). I dunno about question 2. Bear in mind that I've only briefly covered complexity in class, so feel free to prove me wrong. |
|
| Author: | Brightguy [ Wed Sep 21, 2011 3:58 pm ] |
| Post subject: | Re: RE:time complexity and Big-Oh |
Insectoid @ Wed Sep 21, 2011 3:06 pm wrote: The derivatives of 2^(n+1) and 2^n are equal- therefore they are the same complexity (this might not always work and might even be a very bad way to show equivalence).
For one, those derivatives aren't equal... but anyway this isn't really here or there. And in general it won't work if one function is o(1) and the other isn't. |
|
| Author: | Insectoid [ Wed Sep 21, 2011 5:40 pm ] |
| Post subject: | RE:time complexity and Big-Oh |
Ah, my bad. I'm awful at even basic calculus. |
|
| Author: | DemonWasp [ Wed Sep 21, 2011 5:43 pm ] |
| Post subject: | RE:time complexity and Big-Oh |
What IS helpful is that (since |g(x)| > 0) Tony's statement can be reduced to: | f(x) | -------- <= M for all x > x0 | g(x) | Where f(x) = 2 ^ (n+1) and g(x) = 2 ^ (n) . If you write that out on paper, you should be able to spot a simple trick that lets you figure out the value of M. |
|
| Author: | dddx [ Wed Sep 21, 2011 11:49 pm ] |
| Post subject: | Re: time complexity and Big-Oh |
Hi guys, Thank you all for the great help and advise. It seems like i really have to read the whole time complexity again from the beginning since i could not understand many of these things and can't remember a thing on how i did these before and unfortunately in my notes, the prof. jump started to the questions i mentioned without any review... But if anyone still can explain it in a simpler way, i would highly appreciate it Thanks again guys |
|