Computer Science Canada

Scheme TYS
Author:  Hikaru79 [ Sat Nov 18, 2006 1:25 pm ]
Post subject:  Scheme TYS
I'm sure you all know the drill by now Smile I'll get things started!
DISCLAIMER: This TYS, and probably a few others that I'll put up, are shamelessly stolen from my own CS assignments (AFTER the assignment has been handed in, of course Razz). I can't help it, some of these questions are genuinely fun.

PROBLEM 1: A directed graph can be represented as a list of nodes, where each node is a list consisting of a symbol (the node's name) and a list of vertices to its neighbors. For example, the following is a valid graph:
code:
(define Graph
  '((A (B E))
    (B (E F))
    (C (D))
    (D ())
    (E (C F))
    (F (D G))
    (G ())))

And it would look like this:
Posted Image, might have been reduced in size. Click Image to view fullscreen.

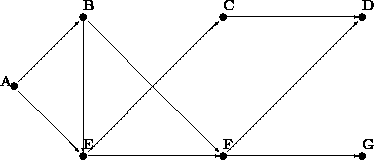
Note that this is a directed graph, so the vertices have a direction; also, the graph may or may not contain cycles (this particular example doesn't, but that's no guarantee).

Write a function that takes a graph and reverses all of its vertices. (ie, if A->B before, now B->A).
For example, reverse-ing the graph we showed before should give
code:
'((A ())
(B (A))
(C (E))
(D (C F))
(E (A B))
(F (B E))
(G (F))))

Which is basically the diagram shown except with all the arrows drawn in the opposite direction.
Author:  Cervantes [ Sat Nov 18, 2006 3:39 pm ]
Post subject: 
**shamelessly steals his answer to this question without doing any additional work**

scheme:

(define (reverse-graph G)
  (map (lambda (x)
         (cons (first x)
               (list (foldr (lambda (a b)
                              (cond
                                [(member (first x) (second a)) (cons (first a) b)]
                                [else b])) empty G)))) G))


Sorry, it's not proper syntax for full scheme. I'd convert it to work in full scheme, but I foldr didn't appear to work. I need some good scheme documentation.
Author:  wtd [ Sat Nov 18, 2006 3:42 pm ]
Post subject: 
code:
datatype node = A | B | C | D | E | F | G;

type graph = (node * node list) list;

val nodes = [A, B, C, D, E, F, G];

fun findNodesThatConsiderNodeNeighbor(n, g) =
   List.map #1 (List.filter (fn (a, ns) => List.exists (fn x => x = n)
                                                       ns)
                            g);

fun reverseGraph(g) =
   List.map (fn n => (n, findNodesThatConsiderNodeNeighbor(n, g))) nodes;
Author:  Hikaru79 [ Sat Nov 18, 2006 3:59 pm ]
Post subject: 
My approach is similar to both of yours'; in fact, almost identical to Cervantes' though I opted for local-define'd functions instead of nested lambda's.

In Dr.Scheme-Scheme:
code:
(define (reverse-graph G)
  (local (
          (define (all-nodes G)
            (map (lambda (l) (first l)) G))
          (define (links-to node G)
            (map first
             (filter (lambda (n) (member node (second n))) G))))
    (map (lambda (n) (cons n (list (links-to n G)))) (all-nodes G))))


And here it is in Standard Scheme:
code:
(define (reverse-graph G)
          (define (all-nodes G)
            (map (lambda (l) (car l)) G))
          (define (links-to node G)
            (map car
             (filter (lambda (n) (member node (cadr n))) G)))
    (map (lambda (n) (cons n (list (links-to n G)))) (all-nodes G)))
Author:  wtd [ Sun Nov 19, 2006 2:11 pm ]
Post subject: 
I'm going to submit a mild variation:

code:
datatype node = A | B | C | D | E | F | G;

type graph = (node * node list) list;

fun allNodes(g : graph) =
   List.map #1 g;

fun findNodesThatConsiderNodeNeighbor(n : node, g : graph) =
   List.map #1 (List.filter (fn (a, ns) => List.exists (fn x => x = n)
                                                       ns)
                            g);

fun reverseGraph(g : graph) =
   List.map (fn n => (n, findNodesThatConsiderNodeNeighbor(n, g)))
            (allNodes(g));

val testGraph =
   [(A, [B, E]),
    (B, [E, F]),
    (C, [D]),
    (D, []),
    (E, [C, F]),
    (F, [D, G]),
    (G, [])];
Author:  Lazy [ Mon Nov 20, 2006 5:26 am ]
Post subject: 
A Haskell solution, worked fine with your test data. It assumes that all nodes are given on the left-hand side, so it'll work with [(A,[B]), (B, [])] but not [(A, [B])].

Node Ids go only to G cos I'm a lazy typist. It would probably be better to use Ints or Chars anyway...

code:
data Node = A | B | C | D | E | F | G
        deriving ( Eq, Show )

type Edge = ( Node, [ Node ] )
type Graph = [ Edge ]

reverseGraph graph = map ( neighbors graph ) ( nodes graph ) where
        nodes =  map fst
        neighbors graph n  =  ( n, map fst $ ( filter $ ( elem n ) . snd ) graph )

-- test data               

testGraph = [   ( A, [ B, E ] ),
                ( B, [ E, F ] ),
                ( C, [ D ] ),
                ( D, [] ),
                ( E, [ C, F ] ),
                ( F, [ D, G ] ),
                ( G, [] ) ]



wtd, is that OCaml you're using? I'm looking for a good comparison of Haskell and OCaml, but my Google Fu is weak... Crying or Very sad
Author:  wtd [ Mon Nov 20, 2006 9:02 am ]
Post subject: 
Actually, in this case it's SML.
Author:  Lazy [ Wed Nov 22, 2006 5:52 am ]
Post subject: 
Any more assignments?
Author:  Hikaru79 [ Sun Dec 03, 2006 7:51 am ]
Post subject: 
Lazy wrote:
Any more assignments?


In retrospect, most of the assignment questions tend to be

a) Too easy for a TYS
b) Too formulaic for a TYS (anyone can look up a graph traversal or implementation of some abstract list function)
c) Too long

However, I have an exam coming up on the 9th, and textbook material tends to get very dry very fast, so if you or wtd want to put up some interesting Scheme challenges, they'd be good preparation Very Happy
Author:  Hikaru79 [ Thu Dec 07, 2006 1:03 pm ]
Post subject: 
Alright, here's another interesting one Smile

Write a function
code:
(define (word-ladder start end dictionary) ... )

that returns a list representing the shortest path from the word "start" to the word "end" with each step in the path being a word in "dictionary" which is exactly one character different from the previous word.

For example, a valid path from "house" to "march" might be
code:
("house" "horse" "morse" "marsh" "march")
assuming, of course, that "horse" "morse" and "marsh" were in dictionary.

There's a rather long list of around 8,000 words that you can use as a wordlist for testing purposes available here Smile

I know this falls rather on the long side for a TYS, though it is possible to do it in around 20 lines. Good luck! Smile (I'll post my solution after a few others have posted)
Author:  Cervantes [ Thu Dec 07, 2006 2:28 pm ]
Post subject: 
20 lines? Pshaah!

Here's my solution, using BST's. I would like to clean up the one-aways function.

scheme:

;; remove-list: (listof X) (listof Y) -> (listof X)
;; removes all elements in `lst2' from `lst1'
;; Definition:
(define (remove-list lst1 lst2)
  (filter (lambda (y) (not (member y lst2))) lst1))


;; union: (listof X) (listof Y) -> (listof (union X Y))
;; removes all elements in lst1 that occur in lst2, then appends the remaining
;; elements onto lst2. If the lists are unique and are thought of as sets,
;; this function is the union operation.
;; Definition:
(define (union lst1 lst2)
  (append lst1 (filter (lambda (x) (not (member x lst1))) lst2)))


;; one-aways: (listof char) -> (listof (listof char))
;; returns a list of lists of characters that are exactly
;; one letter different from `w'
;; Definition:
(define (one-aways w)
  (local ((define (mod-loc w pos new-letter)
            (cond
              [(zero? pos) (cons new-letter (rest w))]
              [else (cons (first w) (mod-loc (rest w) (sub1 pos) new-letter))]))         
          (define (cycle-letter w l pos)
            (cond
              [(= 123 l) empty]
              [else (cons (mod-loc w pos (integer->char l)) (cycle-letter w (add1 l) pos))]))
          (define (cycle-pos w pos)
            (cond
              [(= -1 pos) empty]
              [else (append (cycle-letter w 97 pos) (cycle-pos w (sub1 pos)))])))
    (filter (lambda (x) (not (equal? x w))) (cycle-pos w (sub1 (length w))))))


;; split: (listof X) -> (list (listof X) X (listof X))
;; splits `lst' into a A) list containing the first half,
;; B) the middle element, and C) a list containing the last half
;; Examples: (split '(1 2 3 4 5 6 7)) -> '((1 2 3) 4 (5 6 7))
;; (split '(1 2 3 4)) -> '((1 2) 3 (4))
;; Definition:
(define (split lst)
  (local ((define mid-len (quotient (length lst) 2))
          (define (aux lst0 n first-half)
            (cond
              [(= n mid-len) (list (reverse first-half) (first lst0) (rest lst0))]
              [else (aux (rest lst0) (add1 n) (cons (first lst0) first-half))])))
    (aux lst 0 empty)))


;; A Binary Search Tree (bst) is either
;; 1. empty or
;; 2. a node:
;;  (make-node w lft rgt)
;; where w is a string, lft and rgt are nodes,
;; and (node-word lft) < w < (node-word rgt)
(define-struct node (word left right))

;; ordered-list->bst: (listof X) -> bst
;; creates a binary search tree from the list given in ascending order
;; Definition:
(define (ordered-list->bst lst)
  (cond
    [(empty? lst) empty]
    [else (local ((define parts (split lst)))
            (make-node (second parts)
                       (ordered-list->bst (first parts))
                       (ordered-list->bst (third parts))))]))


;; in-bst?: string bst -> boolean
;; returns true if `item' is found in `bst'. False otherwise
;; Definition:
(define (in-bst? item bst)
  (cond
    [(empty? bst) false]
    [(string=? item (node-word bst)) true]
    [(string>? item (node-word bst)) (in-bst? item (node-right bst))]
    [else (in-bst? item (node-left bst))]))


;; word-ladder2: string string (listof string) -> (union false (listof string))
;; returns a list of strings in `words' starting with `start' and ending with `end',
;; where the n'th string is exactly one letter different from the (n-1)'th string
;; Definition:
(define (word-ladder2 start end wl-bst)
  (local ((define (neighbours w wl-bst)
            (filter (lambda (x) (in-bst? (list->string x) wl-bst))
                    (one-aways w)))
          (define (aux starts end seen wl-bst)
            (cond
              [(empty? starts) false]
              [(equal? (first (first starts)) end)
               (reverse (map list->string (first starts)))]
              [else
               (local ((define nbrs (neighbours (first (first starts)) wl-bst)))
                 (aux (append (rest starts)
                              (map (lambda (x) (cons x (first starts)))
                                   (remove-list nbrs seen)))
                      end
                      (union nbrs seen)
                      wl-bst))])))
    (aux (list (list (string->list start))) (string->list end) empty wl-bst)))

;; Tests:
(define bst-short (ordered-list->bst testwords-short))
(define bst-long (ordered-list->bst testwords-long))
(equal? (word-ladder2 "cat" "dog"
                      (ordered-list->bst (list "cat" "yar" "foo" "cab"
                                               "cot" "god" "dog" "dot")))
        (list "cat" "cot" "dot" "dog"))
(not (word-ladder2 "house" "xerox" bst-short))
(equal? (word-ladder2 "start" "stops" bst-long)
        (list "start" "stare" "store" "stope" "stops"))
Author:  Hikaru79 [ Sun Feb 04, 2007 2:29 am ]
Post subject:  Re: Scheme TYS
Here is another one Smile

One can represent a polynomial as a list of lists, with each element being an ordered pair representing a coefficient and a power of x. For example,
scheme:
'((3 0) (2 2) (4 1) (1 0) (6 1))
represents the equation
code:
3+2x^2+4x+1+6x


Write a function that will take a polynomial in the given form, and represent it in its sparse canonical form; that is, there will be exactly one entry for each non-zero coefficient, in ascending order of degree. For example, the above polynomial has a sparse canonical representation of
scheme:
'((4 0) (10 1) (2 2))


NOTE: If a particular power's coefficient becomes 0 during the simplification, it should not be included in the representation.
Author:  wtd [ Sun Feb 04, 2007 9:50 am ]
Post subject:  RE:Scheme TYS
Because everyone loves reductions...

code:
(define (reduce-polynomial complex-polynomial)
 
  (define (reduce f initial lst)
    (if (null? lst)
        initial
        (reduce f (f initial (car lst)) (cdr lst))))
 
  (define unique-powers
    (reduce (lambda (a b)
              (let ((power (cadr b)))
                (if (memq power a) a (append a (list power)))))
            '()
            complex-polynomial))
 
  (reduce
   (lambda (a b)
     (append a
             (list
              (list
               (reduce
                 (lambda (a2 b2)
                   (let ((power (cadr b2))
                         (coefficient (car b2)))
                     (if (equal? b power) (+ a2 coefficient) a2)))
                 0
                 complex-polynomial)
                b))))
   '()
   unique-powers))
               

(reduce-polynomial '((3 0) (2 2) (4 1) (1 0) (6 1)))
Author:  Hikaru79 [ Sun Feb 04, 2007 10:25 am ]
Post subject:  Re: Scheme TYS
Interesting solution, wtd Smile

However...
scheme:
> (reduce-polynomial '((-1 3) (1 3)))
((0 3))


Coefficients of 0 should drop out; after all, we would never write "0x^3" as a polynomial. The result here should have been the empty list.
Author:  Hikaru79 [ Sun Feb 04, 2007 10:46 am ]
Post subject:  Re: Scheme TYS
Oh, and here's my solution, translated to standard R5RS Scheme. It LOOKS overly long and complicated, but my dirty secret is that remove-duplicates was actually a question on an earlier assignment, which I copied over word-for-word, so the amount of new code I wrote here is actually pretty small Smile (And actually, a lot of Scheme implementations have their own remove-duplicates, so this is not even neccesary.) Two helper functions and then one nice big long convoluted abstract list function.

scheme:
(define (p-canonize f)
      (define (remove-duplicates lst0)
             (define (rd-a accum list)
                (cond
                  ((empty? list) accum)
                  ((member (first list) (rest list))
                   (rd-a accum (rest list)))
                  (else
                   (rd-a (cons (first list) accum)
                         (rest list)))))
           (rd-a empty (reverse lst0)))
       
       (define (get-coeff-list f)
         (foldr (lambda (x y) (cons (second x) y)) empty f))
       
       (define (sum-with-coeff f co)
         (foldr (lambda (x y) (+ (first x) y)) 0 (filter (lambda (x) (= (second x) co)) f)))
       
    (filter (lambda (x) (not (= (first x) 0))) (foldr (lambda (x y) (cons (cons (sum-with-coeff f x) (cons x empty)) y))
           empty (remove-duplicates (get-coeff-list (sort f (lambda (x y) (< (second x) (second y)))))))))


Then we have:
scheme:

> (p-canonize '((1 3) (-1 3)))
()
> (p-canonize '((3 0) (2 2) (4 1) (1 0) (6 1)))
((4 0) (10 1) (2 2))


Note: Hmm, someone should modify the Scheme syntax highlighting file so it doesn't highlight the "list" keyword unless it's got whitespace on both sides...
Author:  Cervantes [ Sun Feb 04, 2007 1:27 pm ]
Post subject:  Re: Scheme TYS
Here's mine, not translated to R5RS.

scheme:

(define (p-canonize sparse-poly)
  (local ((define (aux prev-element ssp)
            (cond
              [(empty? ssp) (cons prev-element empty)]
              [(= (cadr prev-element) (cadar ssp))
               (aux (list (+ (car prev-element) (caar ssp)) (cadr prev-element)) (cdr ssp))]
              [else (cons prev-element (aux (car ssp) (cdr ssp)))])))
    (filter (lambda (x) (not (= 0 (fst x))))
            (aux '(0 0) (sort sparse-poly (lambda (a b) (< (cadr a) (cadr b))))))))
Author:  wtd [ Mon Feb 05, 2007 11:36 pm ]
Post subject:  RE:Scheme TYS
New one. Probably rather simple, but let's see what kind of responses we get. Smile

Write a tail-recursive function split which splits a list into a pair of lists, based on whether or not the members satisfy a predicate.

code:
(split (lambda (x) (< x 2))
       '(0 1 2 3 4 5))


Should result in:

code:
((0 1) (2 3 4 5))
Author:  Cervantes [ Tue Feb 06, 2007 3:08 pm ]
Post subject:  RE:Scheme TYS
Seems like pretty easy accumulative recursion:
scheme:

(define (split pred lst)
  (letrec ((aux
            (lambda (pred lst pass fail)
              (cond
                ((empty? lst) (list pass fail))
                ((pred (car lst)) (aux pred (cdr lst) (cons (car lst) pass) fail))
                (else (aux pred (cdr lst) pass (cons (car lst) fail)))))))
    (aux pred lst empty empty)))

(split (lambda (x) (< x 4)) '(1 2 3 8 4 3 6 9))

This function is useful in implementing a quicksort.
Author:  wtd [ Tue Feb 06, 2007 5:06 pm ]
Post subject:  RE:Scheme TYS
My own solution implemented this in terms of a left -> right reduction. Smile

An O'Caml version:

code:
let split f = List.fold_left (fun (a, a') b -> if f b then (a @ [b], a') else (a, a' @ [b])) ([], [])

:


You can syndicate this boards posts using the file backend.php or view the topic map using sitemap.php.

Terms of Use | Privacy Policy