Stack Overflow and Recursion Depth
| Author |
Message |
np_123
|
 Posted: Sun May 03, 2015 6:16 pm Post subject: Stack Overflow and Recursion Depth Posted: Sun May 03, 2015 6:16 pm Post subject: Stack Overflow and Recursion Depth |
|
|
I tried writing a program that would calculate the value of 'e' (Euler's number) to a large number of decimal places using a formula for rapidly converging infinite series.
The specific formula I used is e = sum of series: (2n +2)/(2n + 1)!
I wanted to see how far I could get with the calculation (within a reasonably short amount of running time) but I keep running into Exception in thread "main" java.lang.StackOverflowError. It seems that it is unable to do factorials for numbers greater than ~12000 and I'm not sure why because as far as I know java.math.BigDecimal has arbitrary(and if unspecified, unlimited I'm pretty sure) precision.
So what I'm wondering can I get rid of this limitation?problem? and have the program run continuously until either it reaches some form of maximum memory consumption or I decide to terminate it?
In case it's relevant, I'm using 64-bit Eclipse IDE, and the below code (though with minor modification) ran for 12500-12600 iterations of the while loop before ending with java.lang.StackOverflowError pointing to this line in the code " out = factorial(rec); ".
|
|
|
|
|
 |
Sponsor
Sponsor


|
|
 |
Zren

|
 Posted: Sun May 03, 2015 8:28 pm Post subject: Re: Stack Overflow and Recursion Depth Posted: Sun May 03, 2015 8:28 pm Post subject: Re: Stack Overflow and Recursion Depth |
|
|
Eh, I'm not sure it's the best idea to give more memory to the stack. Usually when you run into stack overflow errors when doing recursion, it's time to think of solving the problem iteratively.
From what I understand of the calculation of e, you could calculate the factorial iteratively as well.
Eg:
| Python: |
n = 0
fact = 1
e = 1
while True:
n += 1
fact *= n
e += 1 / fact
|
Though your algorithm is a bit different than what I see on wikipedia:
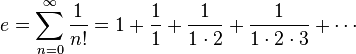
| Python: |
e = 0
count = 0
while True:
recurse = 2 * count + 1
fact = factorial(recurse)
num = (2 * count + 2) / fact
e += num
count += 1
|
Your's seems to be skipping even numbers? And the numerator is 2 * (count+1) instead of 1? Is there a source for this algorithm? |
|
|
|
|
 |
np_123
|
 Posted: Sun May 03, 2015 9:30 pm Post subject: Re: Stack Overflow and Recursion Depth Posted: Sun May 03, 2015 9:30 pm Post subject: Re: Stack Overflow and Recursion Depth |
|
|
Yeah, I do have a source for this algorithm: http://m.intmath.com/exponential-logarithmic-functions/calculating-e.php
The website calls it the Brothers' Formulae. I've used it to calculate e to almost 100000 digits before getting stack overflow so in that sense I can somewhat attest to its correctness.
It never actually occurred to me to calculate the factorial like that - multiplying by the term as the program iterates through the loop. I can see how that would probably be much more efficient than recursion with such large numbers as I'd be dealing with.
And so calculating the factorial iteratively instead of using recursion should avoid the stack overflow error then? If that's the case, then I should be able to get it working without too much extra effort by the sounds of it. |
|
|
|
|
 |
wtd
|
 Posted: Thu May 07, 2015 10:14 am Post subject: RE:Stack Overflow and Recursion Depth Posted: Thu May 07, 2015 10:14 am Post subject: RE:Stack Overflow and Recursion Depth |
|
|
You're not wrong to sue recursion to solve this problem, or Java, but...
You are wrong to use both at the same time.
Java does not implement tail call optimization.
The way the stack works is that every function/method call tacks it's requisite information onto the stack. The deeper you go in the recursion, the larger the stack gets. Enough levels of recursion and BOOM! Stack overflow.
Tail call optimization involves compilers determining that if a function call is the last call in a function, it can eliminate the stack presence of the calling function. Properly designed, a recursive function never uses more stack space than is required for one function call.
A simple example would be calculating factorials recursively.
| code: | let factorial x =
let rec factorial' x acc =
if x = 1 then
acc
else
factorial' (x - 1) (acc * x)
in
factorial' x 1
in
factorial 5 |
And we can sketch out how execution of this would look:
| code: | factorial 5
factorial' 5 1
factorial' 4 5
factorial' 3 20
factorial' 2 60
factorial' 1 120
120 |
Now, a version which doesn't use tail calls and we can see the difference.
| code: | let factorial x =
if x = 0 then
1
else
x * factorial (x - 1)
in
factorial 5 |
Now to look at the execution:
| code: | factorial 5
5 * factorial 4
5 * 4 * factorial 3
5 * 4 * 3 * factorial 2
5 * 4 * 3 * 2 * factorial 1
5 * 4 * 3 * 2 * 1 * factorial 0
5 * 4 * 3 * 2 * 1 * 1
120 |
Obviously that won't overflow the stack, but imagine if we'd used a much larger number, or had a more complex recursive function.
In short, if you wish to continue using Java, find a way to iteratively calculate, rather than relying on recursion.
Or learn another language. It's fun! |
|
|
|
|
 |
np_123
|
 Posted: Thu May 07, 2015 7:02 pm Post subject: Re: Stack Overflow and Recursion Depth Posted: Thu May 07, 2015 7:02 pm Post subject: Re: Stack Overflow and Recursion Depth |
|
|
I changed it to calculate the factorial iteratively using a while loop and repeated multiplication and I must say its quite very extremely slow once it starts reaching numbers in the several thousands. Still, I wasn't expecting it to run fast, and I learned fair amount along the way, so it served its purpose.
Now I'm thinking to see if I can write code to do the same job(but hopefully a lot better) in C++. And in place of Java's BigDecimal, likely going to use 'GNU multiple precision arithmetic library'(gmp) to get the higher precision. |
|
|
|
|
 |
wtd
|
 Posted: Fri May 08, 2015 12:48 am Post subject: RE:Stack Overflow and Recursion Depth Posted: Fri May 08, 2015 12:48 am Post subject: RE:Stack Overflow and Recursion Depth |
|
|
For fun, I rewrote my function to handle 64-bit integers.
| code: | open Big_int;;
include Big_int;;
let factorial x =
let rec factorial' x acc =
if eq_big_int x 0I then
acc
else
factorial' (sub_big_int x 1I) (mult_big_int x acc)
in
factorial' (big_int_of_int x) 1I;; |
|
|
|
|
|
 |
|
|

